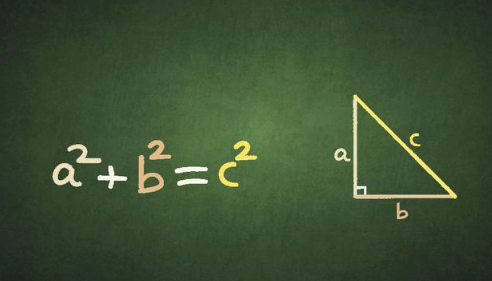Mengenal Rumus Phytagoras dan Contoh Soalnya

Rumus Phytagoras – Dalam panorama matematika yang luas, satu rumus menjadi batu penjuru, membimbing kita melalui ranah segitiga dan sudut-sudut siku – Teorema Pythagoras yang perkasa. Artikel ini merambah ke dalam pemahaman yang mendalam, membongkar nuansa dari “Mengenal Rumus Phytagoras dan Contoh Soalnya” (Getting to Know the Pythagorean Formula and its Example Problems). Bersiaplah untuk perjalanan pencerahan melalui tanah angka dan keajaiban geometris.

Table of Contents

Mengungkap Dasar-Dasar Rumus Phytagoras

“Mengenal Rumus Phytagoras dan Contoh Soalnya” membawa kita ke konsep dasar yang dirancang oleh matematikawan Yunani kuno, Pythagoras. Rumus ini dengan elegan menghubungkan panjang sisi-sisi segitiga siku-siku: a2+b2=c2. Di sini, c mewakili hipotenusa, sedangkan a dan b adalah kaki segitiga. Kesederhanaan persamaan ini menyembunyikan aplikasi mendalamnya dalam berbagai skenario matematika dan dunia nyata.

Aplikasi di Dunia Nyata Rumus Phytagoras

Peran Teorema Pythagoras dalam Konstruksi

Teorema Pythagoras, atau yang dikenal sebagai “Mengenal Rumus Phytagoras dan Contoh Soalnya,” memegang peran kunci dalam dunia konstruksi. Sejak zaman kuno, para arsitek dan insinyur telah mengandalkan rumus ini untuk memastikan kestabilan struktural dalam pembangunan berbagai bangunan. Mari kita telusuri lebih jauh bagaimana teorema ini memainkan peran sentral dalam konstruksi modern.

1. Perhitungan Jarak dan Dimensi

Salah satu aplikasi utama Teorema Pythagoras dalam konstruksi adalah perhitungan jarak dan dimensi. Saat merancang bangunan, arsitek harus memastikan bahwa struktur tersebut seimbang dan tidak terpengaruh oleh ketidaksetaraan panjang sisi-sisi segitiga di dalamnya. Dengan “Mengenal Rumus Phytagoras dan Contoh Soalnya,” para profesional konstruksi dapat menghitung panjang diagonal, memastikan bahwa setiap elemen bangunan ditempatkan dengan presisi matematis.

2. Penentuan Sudut dan Perencanaan Tata Letak

Teorema Pythagoras juga memberikan kontribusi besar dalam menentukan sudut-sudut yang optimal dalam desain konstruksi. Ketika merencanakan tata letak atau penempatan elemen-elemen penting, seperti dinding atau tiang, rumus ini digunakan untuk mengukur jarak secara efisien. Dengan demikian, bangunan dapat dirancang dengan presisi matematis, menciptakan ruang yang efisien dan estetika yang seimbang.

3. Keandalan Struktural

Aspek kritis dalam konstruksi adalah keandalan struktural, yakni kemampuan suatu bangunan untuk menahan beban dan tekanan yang dikenakan padanya. Teorema Pythagoras menjadi alat penting dalam mengukur dan mengonfirmasi kekuatan struktural suatu bangunan. Dengan merinci panjang sisi-sisi segitiga di dalamnya, insinyur dapat memastikan bahwa fondasi dan struktur pendukung lainnya dirancang dengan benar untuk menjamin keamanan jangka panjang.

4. Pemodelan dan Desain Bangunan

Dalam era desain digital, Teorema Pythagoras tetap relevan dalam pemodelan dan desain bangunan menggunakan perangkat lunak CAD (Computer-Aided Design). Profesional desain menggunakan rumus ini untuk merancang ruang yang optimal dan efisien, memastikan bahwa setiap elemen bangunan ditempatkan dengan akurasi matematis, menghasilkan struktur yang kokoh dan efisien.

5. Konstruksi Rute dan Akses

Dalam proyek konstruksi yang melibatkan rute atau akses, seperti jalan atau jembatan, Teorema Pythagoras menjadi panduan tak tergantikan. Pengukuran panjang dan jarak antara titik-titik kritis dilakukan dengan menggunakan rumus ini. Hasilnya adalah sistem transportasi yang efisien dan terukur, memastikan bahwa setiap elemen infrastruktur terintegrasi secara matematis.

6. Teknologi Modern dan Teorema Pythagoras

Dalam era teknologi modern, peralatan pengukuran dan pemetaan yang canggih menggunakan prinsip-prinsip Teorema Pythagoras. Dengan menggunakan teknologi laser dan perangkat lunak pemodelan 3D, para profesional konstruksi dapat mengintegrasikan data dengan akurasi tinggi, menciptakan bangunan yang memenuhi standar keamanan dan presisi matematis.

Dengan demikian, peran Teorema Pythagoras dalam konstruksi tidak hanya menjadi warisan dari masa lalu, tetapi juga tetap menjadi landasan penting dalam menciptakan bangunan-bangunan masa kini yang kokoh, efisien, dan terukur secara matematis.

Aplikasi Nautika Rumus Phytagoras

“Mengenal Rumus Phytagoras dan Contoh Soalnya” memiliki peran yang sangat penting dalam dunia nautika, membantu para pelaut dan navigator untuk melakukan perhitungan yang presisi dalam menavigasi lautan. Berikut adalah beberapa aplikasi nautika yang mengandalkan pada Rumus Phytagoras:

Perhitungan Jarak Antar Titik di Lautan
Salah satu aplikasi utama Rumus Phytagoras dalam nautika adalah untuk menghitung jarak antara dua titik di lautan. Dengan menggunakan panjang sisi-sisi segitiga yang dihasilkan oleh garis lurus antara dua posisi, pelaut dapat dengan cepat dan akurat menentukan jarak yang ditempuh.
Bestarisasi dan Penentuan Arah
Untuk menghindari navigasi yang keliru, pelaut sering kali harus menentukan sudut atau bestarisasi dari satu titik ke titik lainnya. Rumus Phytagoras membantu dalam mengukur sudut ini, memastikan bahwa kapal berlayar pada jalur yang tepat sesuai dengan kompas nautika.
Keamanan Navigasi dan Menghindari Rintangan
Dalam menghindari rintangan di lautan, seperti pulau atau karang, navigator menggunakan Rumus Phytagoras untuk mengukur jarak dengan tepat. Dengan mengetahui jarak ke rintangan, mereka dapat dengan hati-hati merencanakan rute untuk menghindarinya, memastikan keselamatan kapal dan seluruh kru.
Pencarian Lokasi atau Benda Tenggelam
Dalam situasi pencarian dan penyelamatan di laut, Rumus Phytagoras menjadi alat yang penting. Dengan mengetahui posisi awal dan melibatkan pergerakan kapal, para penyelamat dapat menghitung area yang perlu dicari dengan presisi matematis, meningkatkan peluang menemukan lokasi atau benda yang tenggelam.
Pelacakan dan Pengawasan Lalu Lintas Laut
Ketika beroperasi di perairan yang padat lalu lintas, penting bagi kapal untuk mempertahankan jarak yang aman antara satu sama lain. Rumus Phytagoras digunakan untuk mengukur jarak relatif dan memastikan navigasi yang aman di sekitar kapal lain, mencegah kemungkinan tabrakan.
Pemetaan Dasar Lautan
Dalam pemetaan dasar laut, perhitungan kedalaman laut menggunakan Rumus Phytagoras membantu dalam menyajikan gambaran yang akurat tentang topografi dasar laut. Informasi ini sangat penting untuk navigasi yang aman, terutama di perairan yang belum dipetakan dengan baik.

Contoh Soal Mengenal Rumus Phytagoras

Contoh Soal Rumus Phytagoras

Mari kita telusuri pemecahan masalah praktis dengan “Mengenal Rumus Phytagoras dan Contoh Soalnya”. Bayangkan situasi di mana Anda perlu menemukan panjang tangga yang bersandar pada dinding. Dengan Teorema Pythagoras, Anda dapat dengan mudah menghitungnya, memastikan presisi dalam berbagai situasi sehari-hari.

Mengaplikasikan Rumus Phytagoras dalam Geometri

Para pecinta geometri bersorak, karena Teorema Pythagoras adalah teman setia Anda dalam mengungkap teka-teki spasial. Baik menentukan diagonal suatu persegi panjang atau memahami hubungan antar sudut, Mengenal Rumus Phytagoras menerangi jalan menuju pencerahan geometris.

Wawasan Lanjutan ke dalam Rumus Phytagoras

Melampaui Segitiga Siku-siku: Generalisasi Rumus Phytagoras

Meskipun secara tradisional terkait dengan segitiga siku-siku, “Mengenal Rumus Phytagoras dan Contoh Soalnya” memperluas pengaruhnya pada segitiga non-siku. Temukan nuansa generalisasi rumus ini, membuka pintu ke spektrum yang lebih luas dalam penyelesaian masalah geometris.

Koneksi Trigonometri: Rumus Phytagoras dalam Lanskap Trigonometri

Menggali trigonometri, kita temukan koneksi intim antara Teorema Pythagoras dan fungsi trigonometri. Fungsi sinus, kosinus, dan tangen menemukan akarnya dalam prinsip yang tertanam dalam rumus ikonik ini, menambahkan lapisan kompleksitas dan keindahan pada eksplorasi matematis.

Tips dan Trik Menguasai Rumus Phytagoras

Tips Praktis untuk Aplikasi Efektif

Untuk menguasai “Mengenal Rumus Phytagoras dan Contoh Soalnya,” penting untuk mendekati masalah secara sistematis. Break down skenario kompleks menjadi langkah-langkah yang dapat dikelola, identifikasi kaki dan hipotenusa segitiga, dan terapkan rumus dengan presisi. Praktik, seperti yang dikatakan, membuat sempurna, jadi nikmatilah berbagai latihan pemecahan masalah untuk memperkokoh pemahaman Anda.

Membuat Rumus Phytagoras Menjadi Ingatan

Menavigasi kerumitan Mengenal Rumus Phytagoras menjadi lebih mudah dengan bantuan mnemonik. Ciptakan frasa atau asosiasi yang mudah diingat untuk mengingat rumus dengan mudah. Mnemonik mengubah konsep matematika abstrak menjadi jalan pintas mental, membentuk koneksi yang lebih dalam dengan Teorema Pythagoras.

Sebagai kesimpulan, “Mengenal Rumus Phytagoras dan Contoh Soalnya” melampaui ranah matematika, menjadi cahaya pemandu dalam aplikasi praktis dan eksplorasi teoritis. Kelembutan Teorema Pythagoras tidak hanya terletak pada kesederhanaannya, tetapi pada keluwesannya, membentuk dunia di sekitar kita dengan cara yang terlihat dan tak terlihat. Saat Anda memulai perjalanan matematis Anda, biarkan essensi Rumus Phytagoras menjadi kompas Anda, membimbing Anda melalui